Trigonometria esférica

	Trigonometria
	História ; Funções; Funções inversas ; Aprofundamento ;
	Referência
	Lista de identidades ; CORDIC
	Teoria euclidiana
	Lei dos senos ; Lei dos cossenos ; Lei das tangentes ; Teorema de Pitágoras
	Cálculo
	Integração trigonométrica ; Substituição trigonométrica ; Integrais de funções ; Diferenciação trigonométrica ; ;

Em matemática, a trigonometria esférica estuda as propriedades geométricas dos triângulos esféricos, em especial as relações que envolvem ângulos esféricos e arcos esféricos. É a área da geometria esférica que estuda os polígonos que se formam sobre a superfície das esferas, em especial, os triângulos. O estudo de trigonometria esférica tem especial relevância em náutica e navegação para determinar a posição de uma embarcação em alto-mar mediante a observação dos corpos celestes além de emprego na área ‘’design’’ de bola esportivas.

A esfera

Uma esfera E, de centro no ponto (a,b,c) e raio k, é domínio de R³ definido por todos pontos no espaço tridimensional que cumprem com a seguinte definição:

$E=\{\ (x,y,z)\in \mathbb {R} ^{3}\ |\ (x-a)^{2}+(y-b)^{2}+(z-c)^{2}=k^{2}\}.$

Círculo máximo

A intersecção de uma esfera com um plano que contenha seu centro gera um círculo máximo e uma circunferência máxima sobre a superfície da esfera. Um círculo máximo divide a esfera em dois hemisférios iguais. A distância entre dois pontos da superfície da esfera, unidos por um arco de círculo máximo, é a menor entre eles, e denomina-se distancia ortodrômica. Como exemplos de círculos máximos, temos na superfície terrestre os meridianos e a linha do equador.

Volume e superfície das esferas

O volume de uma esfera é o volume de revolução produzida por um semi círculo que gira ao redor do diâmetro. Segundo esta definição, se o seu raio é r, seu volume será:

$V={\frac {4}{3}}\pi r^{3}.$

A superfície é a superfície lateral de um corpo de revolução e será dada por:

$A=4\pi r^{2}.$

Domínio sobre a superfície esférica

Um domínio de superfície esférica é uma área sobre a superfície da esfera, limitado pela curvas dessa superfície.

Triângulo esférico

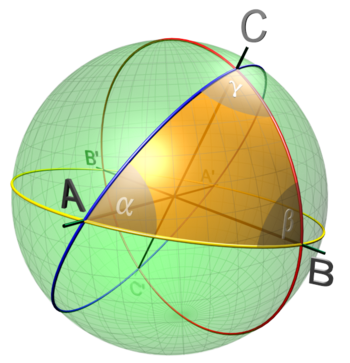
Se três pontos da superfície esférica são unidos por arcos de círculo máximo, menores que 180º, a figura obtida denomina-se triângulo esférico. Os lados do polígono assim formado se expressam por conveniência como ângulos cujos vértices são o centro da esfera e não por sua longitude. Este arco medido em radianos e multiplicado pelo raio da esfera é a longitude do arco. Em um triângulo esférico os ângulos cumprem que: 180° < $\alpha$ + $\beta$ + $\gamma$ < 540°.

Fórmulas fundamentais

$\alpha :$ ângulo formado entre os arcos AC e AB
$\beta :$ ângulo formado entre os arcos AB e BC
$\gamma :$ ângulo formado entre os arcos AC e BC

Fórmula do cosseno

$\cos CB=\cos AC\;\cos AB+{\rm {sen}}AC\;{\rm {sen}}AB\;\cos \alpha$

Fórmula do seno

${\frac {{\rm {sen}}CB}{{\rm {sen}}\alpha }}={\frac {{\rm {sen}}AC}{{\rm {sen}}\beta }}={\frac {{\rm {sen}}AB}{{\rm {sen}}\gamma }}$

Os senos dos lados são proporcionais a os senos dos ângulos opostos.

Fórmula da cotangente

A fórmula da cotangente também se denomina fórmula de elementos consecutivos. Ver na figura os seguintes elementos consecutivos:

ângulo $\alpha ;$ lado $AB;$ ângulo $\beta ;$ lado $BC.$

$\cos \beta \cos AB=-{\rm {sen}}\beta \cot \alpha \!+{\rm {sen}}AB\cot CB$

Cosseno dos elementos centrais é igual a: menos seno do ângulo médio pela cotangente do outro ângulo.

Fórmula de Bessel

Das fórmulas dos cossenos, obtendo a seção posterior, pode-se obter de imediato um conjunto de várias fórmulas conhecidas como "relações de seno por cosseno" ou também denominadas Fórmulas de Bessel, especialmente a terceira fórmula de Bessel. Foram deduzidas pela primeira vez pelo matemático Friedrich Wilhelm Bessel.

$\cos(a/k)=\cos(b/k)\cdot \cos(c/k)+\mathrm {sen} \,(b/k)\cdot \mathrm {sen} \,(c/k)\cdot \cos(A)$

$\cos(b/k)=\cos(c/k)\cdot \cos(a/k)+\mathrm {sen} \,(c/k)\cdot \mathrm {sen} \,(a/k)\cdot \cos(B)$

$\cos(c/k)=\cos(a/k)\cdot \cos(b/k)+\mathrm {sen} \,(a/k)\cdot \mathrm {sen} \,(b/k)\cdot \cos(C)$

O conjunto das fórmulas de Bessel pode descrever para a esfera de raio unitário, isto é, a esfera trigonométrica, da forma:

$\mathrm {sen} \,c\cdot \cos B=\cos b\cdot \mathrm {sen} \,a-\cos a\cdot \mathrm {sen} \,b\cdot \cos C$
$\mathrm {sen} \,c\cdot \cos A=\cos a\cdot \mathrm {sen} \,b-\cos b\cdot \mathrm {sen} \,a\cdot \cos C$
$\mathrm {sen} \,b\cdot \cos A=\cos a\cdot \mathrm {sen} \,c-\cos c\cdot \mathrm {sen} \,a\cdot \cos B$
$\mathrm {sen} \,b\cdot \cos C=\cos c\cdot \mathrm {sen} \,a-\cos a\cdot \mathrm {sen} \,c\cdot \cos B$
$\mathrm {sen} \,a\cdot \cos B=\cos b\cdot \mathrm {sen} \,c-\cos c\cdot \mathrm {sen} \,b\cdot \cos A$
$\mathrm {sen} \,a\cdot \cos C=\cos c\cdot \mathrm {sen} \,b-\cos b\cdot \mathrm {sen} \,c\cdot \cos A$

Matrizes das fórmulas de um triângulo esférico

O conjunto das fórmulas do seno, do cosseno (conhecido por alguns como segunda e primeira fórmula de Bessel), e a tercei fórmula de Bessel, podem ser expressas da seguinte forma matricial:

${\begin{vmatrix}\cos(a)\\\mathrm {sen} \,(a)\mathrm {sen} \,(B)\\\mathrm {sen} \,(a)\cos(B)\end{vmatrix}}={\begin{vmatrix}\cos(c)&0&\mathrm {sen} \,(c)\\0&1&0\\\mathrm {sen} \,(c)&0&-cos(c)\end{vmatrix}}.{\begin{vmatrix}\cos(b)\\\mathrm {sen} \,(b)\mathrm {sen} \,(A)\\\mathrm {sen} \,(b)\cos(A)\end{vmatrix}}$

sendo a, b y c os lados; y A, B y C os ângulos do triângulo esférico.

Triângulo esférico retângulo

O triângulo esférico com pelo menos um ângulo reto se denomina triângulo retângulo. Em um triângulo esférico seus três ângulos podem ser retos, em cujo caso, a soma é 270°. Em todos os outros casos essa soma excede os 180° e a esse excesso se denomina excesso esférico; se expressa pela fórmula: E: E = $\alpha$ + $\beta$ + $\gamma$ - 180°.

Qualquer triângulo esférico pode descompor-se em dois triângulos esféricos retângulos.

Pentágono de Napier

O pentágono de Napier é uma regra mnemónica para resolver triângulos esféricos retângulos; tem esse nome em memória do cientista inglês John Napier, e se constrói da seguinte forma:

Coloca-se em cada setor circular: cateto - ângulo - cateto - ângulo - cateto, consecutivamente, tal como aparecem ordenados no triângulo, exceto o ângulo reto C.

Se assinalam os ângulos B, A, e a hipotenusa c por seus complementares:

B por (90° - B)

A por (90° - A)

c por (90° - c)

Estabelecem-se as seguintes regras:

O seno de um elemento é igual o produto das tangentes dos elementos adjacentes:
seno(a) = tg(b) tg(90° - B), ou seu equivalente: seno(a) = tg(b) ctg(B)
O seno de um elemento é igual ao produto dos cossenos dos elementos opostos:
seno(a) = cosseno(90° - A) cosseno(90° - c), ou seu equivalente: seno(a) = seno(A) seno(c)

Ver também

Bibliografia

Apuntes de Trigonometría esférica. Universidad de Cádiz. (em castelhano)
Astronomía Náutica (tomo primero). Luis Virgile. Imprenta Escuela Naval Militar (Argentina). (em castelhano)

Ligações externas

O Commons possui uma categoria com imagens e outros ficheiros sobre Trigonometria esférica

(em inglês) Great Circle Calculator
(em inglês) Matemática del Círculo Máximo
(em português) "O Livro de Instruções sobre Planos Desviantes e Planos Simples" é um manuscrito em árabe que remonta a 1740 e fala sobre trigonometria esférica, com diagramas.